Discretized Boosted Decision Trees for High-Speed FPGA-Optimized Digit Recognition

This work is my submission for the Digit Recognition Low Power and Speed Challenge @ ICIP 2025. The original pdf version of this paper can be downloaded here.

Abstract

This paper presents a high-speed, FPGA-optimized implementation of boosted decision trees for handwritten digit recognition on the MNIST dataset, achieving a test set accuracy of 97.73% and a throughput of 640 million images per second on a Cyclone V FPGA. By binarizing input images and discretizing decision tree leaf scores, the design efficiently leverages FPGA hardware primitives without any floating-point operations. Each decision tree leaf node is implemented as a single lookup table, outputting high when active. Leaf node outputs are aggregated by counting active nodes per discrete value and summing them in a common base. Leaf score discretization is performed after each boosted tree training iteration, enabling subsequent trees to correct these discretization errors. A four-core pipelined architecture, operating at 160 MHz, consumes 625 mW of power, achieving an efficiency of 1.02 billion images per second per watt. This paper is submitted to the Digit Recognition Low Power and Speed Challenge @ ICIP 2025.

This work is open source and available at github.com/martinloretzzz/mnist-fpga/.

Introduction

The Digit Recognition Low Power and Speed Challenge aims to find the fastest and most energy-efficient FPGA-based hardware accelerator for handwritten digit recognition on the MNIST dataset [1], targeting a test set accuracy exceeding 97.5%. To maximize throughput, we aim for the smallest model that meets this accuracy threshold. While multilayer perceptrons (MLPs) and convolutional neural networks (CNNs) can easily achieve this accuracy, their models typically contain tens or hundreds of thousands of parameters and rely on floating-point arithmetic, making them suboptimal for fast FPGA implementations.

Tree-based models offer a compelling alternative due to their compact size and computational efficiency. Among these, boosted trees [2] stand out, achieving up to 98.2% accuracy with some parameter tuning, while we were unable to reach the accuracy threshold with other tree-based methods.

Rather than designing a generic runtime that can run any boosted tree, we aim to hardwire the entire model on an FPGA into one block of combinatorial logic that processes one image per clock cycle. To fit the boosted tree into the limited number of logic units available on an FPGA, we modify the boosted trees to effectively use the hardware primitives of FPGAs.

Discrete Boosted Trees

To optimize boosted trees for FPGAs, we eliminate all floating-point operations, as these require floating-point units that are slow and resource-intensive. Floating-point values appear in two places: the input image and the decision tree leaf scores.

For the input image, we binarize it using a fixed threshold to convert grayscale images into binary (black or white) pixels. Experimental results indicate that a threshold of 0.3 works best for MNIST. This binarization eliminates the need for comparators in decision nodes, as inputs are already binary.

Discretizing leaf scores is more complex, as post-training discretization would introduce significant errors. Boosted trees are trained sequentially, one after another, with later trees correcting the errors of earlier ones. This property enables discretization after each iteration when a tree is trained, allowing later trees to compensate for those discretization errors.

The distribution of leaf scores is visualized in this histogram (for non-discretized trees):

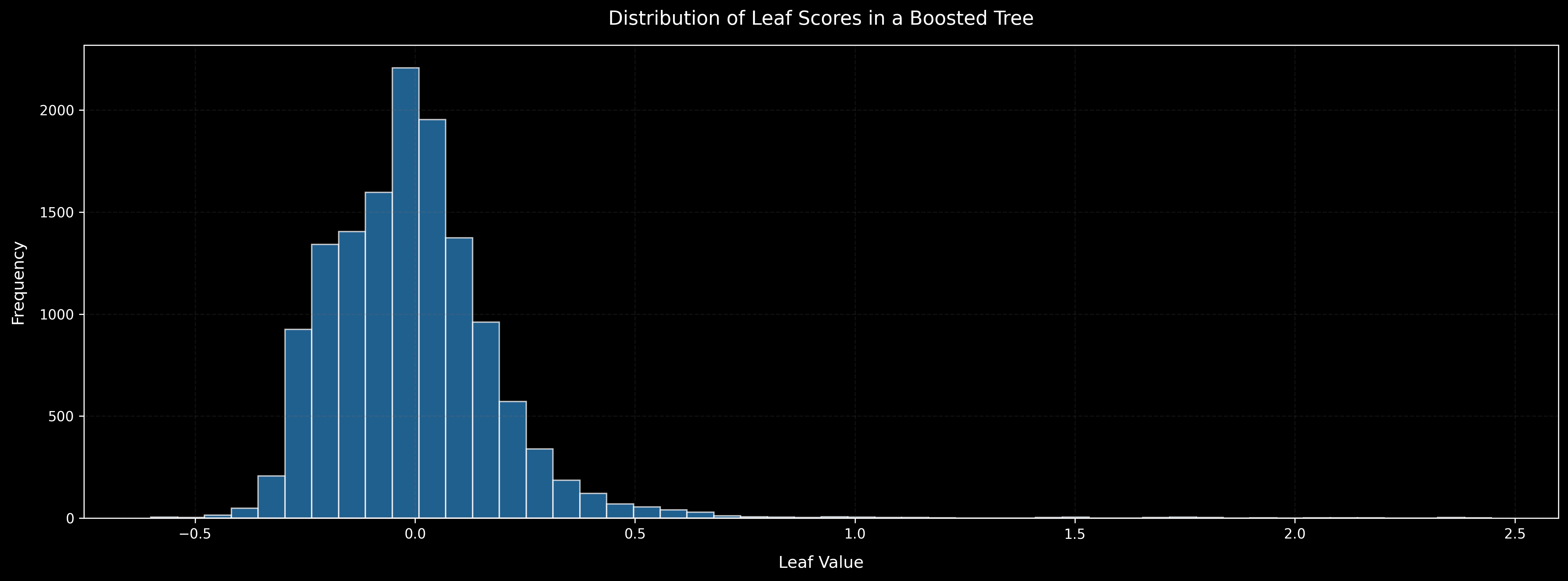
While the trees of the first iterations have larger scores, the magnitude of these scores decreases rapidly, with later trees contributing less to the total score. Based on this distribution, we propose this set of discrete values: { -1/4, -1/8, -1/16, -1/32, -1/64, 0, 1/64, 1/32, 1/16, 1/8, 1/4, 1/2, 1, 2 }.

This set enables a binary-like series expansion for intermediate values by combining multiple decision trees with identical conditions in sequence; whether the model uses this capability can be investigated in future work.

To implement this discretization, we forked the XGBoost library [3] (github.com/martinloretzzz/xgboost) and modified it to adjust leaf scores after each iteration. Positive leaf scores are rounded down to the nearest discrete value less than or equal to the exact score, while negative scores are rounded up to the nearest discrete value greater than or equal to the exact score.

The impact of this discretization on accuracy is minimal. For smaller trees, a slight reduction in accuracy is observed, whereas for larger trees, accuracy improves slightly. Investigating the reason for this improvement is a topic for future work.

Number of Estimators	Accuracy Exact %	Accuracy Discrete %
100	97.84	97.75
150	97.98	98.05
200	98.06	98.14

FPGA-Optimized Boosted Tree Implementation

This implementation optimizes a boosted tree that consists of 10 classifiers, each with 100 decision trees as estimators and a maximum depth of four.

Each decision tree generates a binary vector of up to 16 elements (2^4), one-hot encoding the active leaf node based on the binary pixel values of the input image. Each leaf node is implemented using a 4-input lookup table (LUT), where all conditions along the path are connected by AND gates.

For example, in this two-layer decision tree, leaf nodes are represented by the following Boolean expressions:

$L_1 = \neg A \land \neg B$
$L_2 = \neg A \land B$
$L_3 = A \land \neg C$
$L_4 = A \land C$

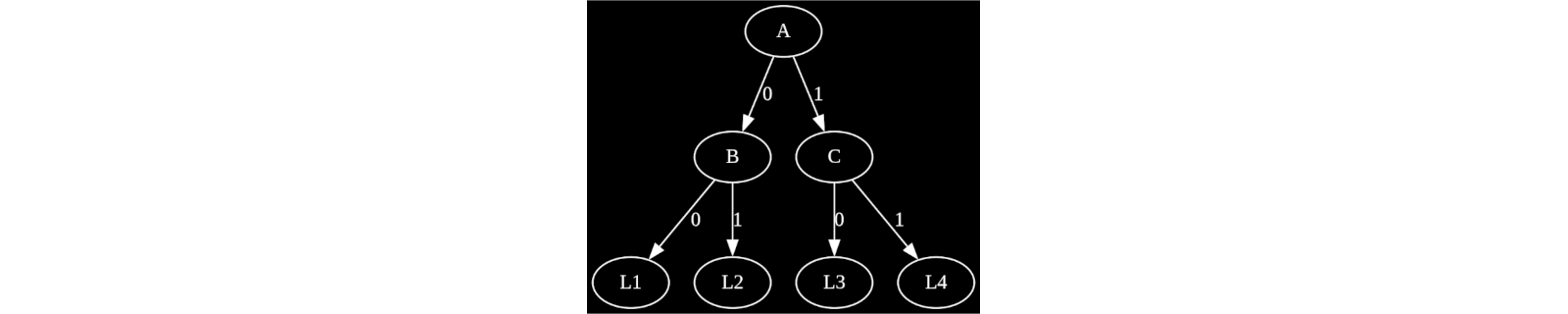
This approach allows the implementation of all decision tree leaves of the MNIST classifier using 16,000 4-input LUTs. By accounting for shallower leaves and excluding zero-score ones, this total number is reduced to approximately 12,500 LUTs.

Since only one leaf node per tree is active at a time and the set of discrete values is small, we can further optimize by OR-connecting all leaf nodes with the same discrete value inside a tree to output whether the tree uses that specific value. The compiler optimizes these OR connected leaves to LUTs with more than 4 inputs and reduces the total number of LUTs needed for all trees to approximately 6,000.

Next, we sum the leaf values of all active leaf nodes. Without discretization, we could quantize them and use a large integer adder, but this would consume most, if not all, FPGA resources.

With the discrete values instead, we can count the number of active leaf nodes for each discrete value, effectively counting active bits in a vector. These counts are then converted to a common base of 0.25 with bit shifts (enabled by the choice of the discrete values) and summed to compute the classifier’s score. The counters are implemented as parallel prefix adders.

The predicted digit is then determined by identifying the classifier with the highest score, using a four-step comparison tree.

See the appendix for a detailed example of these calculations.

The entire boosted tree implementation forms a single block of combinatorial logic, processing one image per clock cycle (at 25 MHz). To increase throughput, we split the design into smaller stages to pipeline it. For the highest throughput classifier, we use 16 pipeline stages with a clock rate of 160 MHz, leading to a latency of 100 ns. A single MNIST classifier only utilizes 22% of the available logic units of the FPGA, so the design is synthesized four times to process four images per clock cycle.

The FPGA implementation’s accuracy of 97.73% on the MNIST test set is slightly lower than the 97.75% of the discretized model running with the XGBoost library, likely due to rounding errors during the conversion of the value counts to the common base.

For a clearer understanding of the implementation, refer to the simple-pipelined tagged version, which provides a four-stage pipelined design. The 16-stage pipelined, four-core implementation used for the results is available in the master branch.

Results

Metric	Value
FPGA	Cyclone V (5CEFA7F31I7)
Logic utilization	51,015 / 56,480 ALM (90%)
Accuracy	97.73%
Clock Rate	160 MHz
Setup Slack*	0.052 ns
Cores	4
Throughput	640 Mimg/s
Latency	16 clock cycles (100 ns)
Power	624.90 mW
Images detections per second per watt	1024.1 Mimg/s/W

* Slow 1100mV -40°C (worst case)

To reproduce these results, follow the steps described in the Readme.md

Conclusion

This work presents an FPGA-optimized implementation of boosted decision trees for MNIST handwritten digit recognition, achieving a test set accuracy of 97.73% while processing 640 million images per second. By discretizing the leaf scores during training and binarizing input images, we can efficiently leverage FPGA hardware primitives with minimal accuracy loss.

This approach is applicable to accelerate boosted trees on FPGAs when inputs can be binarized with negligible information loss. These results demonstrate the potential of hardware-accelerated machine learning models for high-speed inference in resource-constrained, low-power environments. Future work could eliminate the binarization constraint by quantizing the input and using comparators in the decision trees.

This design achieves an efficiency of 1.02 billion images per second per watt.

References

[1]: LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324. https://doi.org/10.1109/5.726791

[2]: Hastie, T.; Tibshirani, R.; Friedman, J. H. (2009). "10. Boosting and Additive Trees". The Elements of Statistical Learning (2nd ed.). New York: Springer. pp. 337–384. ISBN 978-0-387-84857-0.

[3]: Chen, T., & Guestrin, C. (2016). XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 785–794). New York, NY, USA: ACM. https://doi.org/10.1145/2939672.2939785

Appendix: Example Calculation

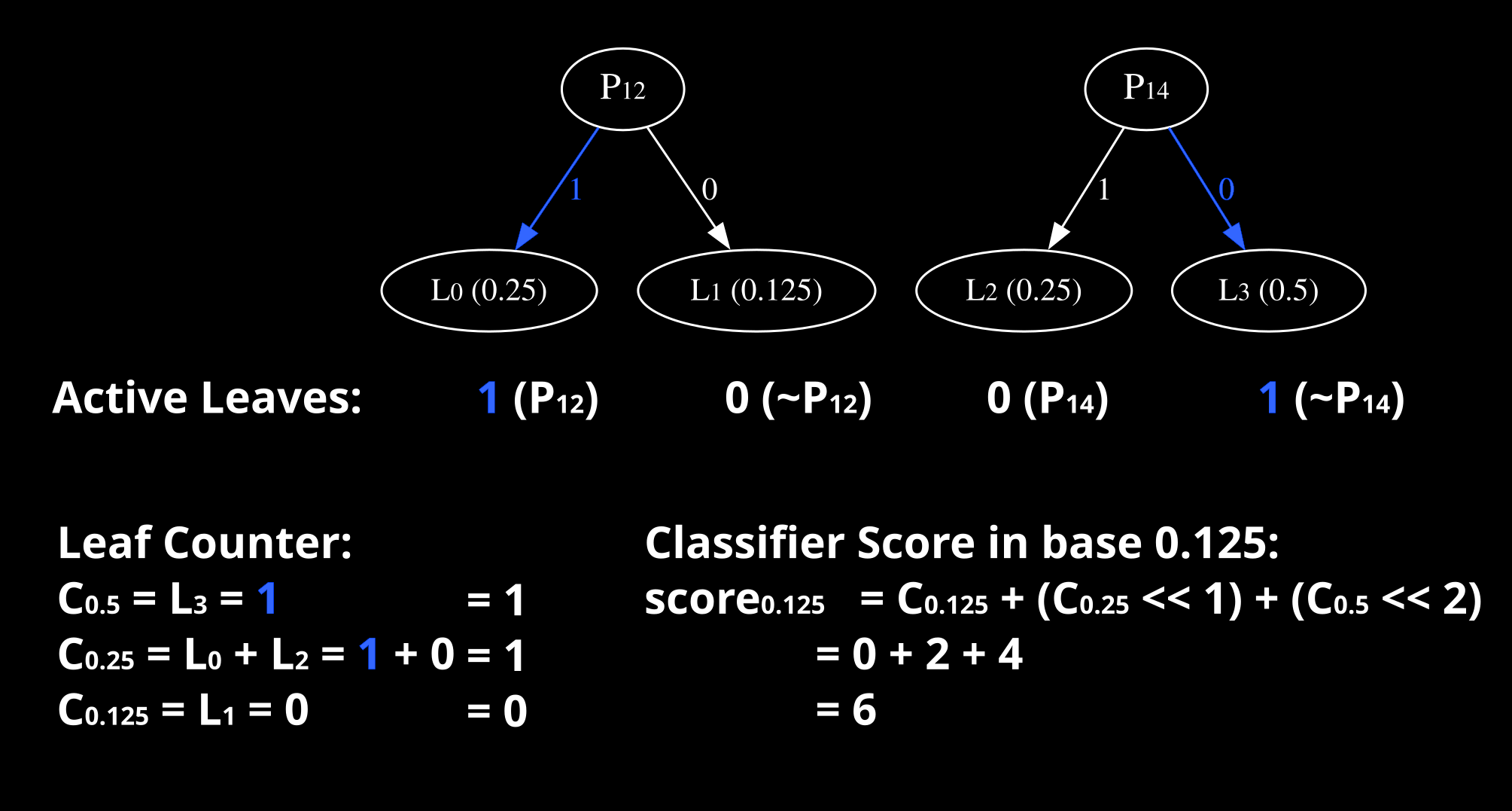
This example illustrates the calculation process for predicting the score of a single digit using two single-layer decision trees. The process involves three main steps:

1. Determining Active Leaves: We first identify the active leaves in the boosted tree based on the input image. For this example, consider an input where pixel $P_{12} = True$ and $P_{14}​ = False$. These conditions activate leaves $L_0$ and $L_3$​ (decision_trees.sv).
2. Aggregating Active Leaves: The active leaves are counted for each discrete value using the equations defined above for $C_{0.5}$, $C_{0.25}$​, and $C_{0.125}$​ (leaf_counters.sv).
3. Computing the Final Score: The counts are converted to a common base, in this case, 0.125, and summed to compute the classifier’s score. In this example, the resulting score is 6 (counter_adder.sv).

This process is repeated for the classifiers of the 9 other digits, and the digit with the highest score is selected as the final prediction (max_value_index.sv, mnist_classifier.sv).