Exploring the activation ratios of different MLP layers

As part of some ongoing work, I've become interested in understanding how many neurons in a layer (Linear + ReLU) actually contribute to the next layer versus those that remain inactive after the activation function (their output being zero).

Activation ratio

To quantify this, we define the activation ratio as follows:

$\text{Activation Ratio} = \frac{\text{Number of activated neurons}}{\text{Total number of neurons}} = \frac{\sum_{i=1}^{N} \mathbb{1}(a_i > 0)}{N}$

MNIST classification

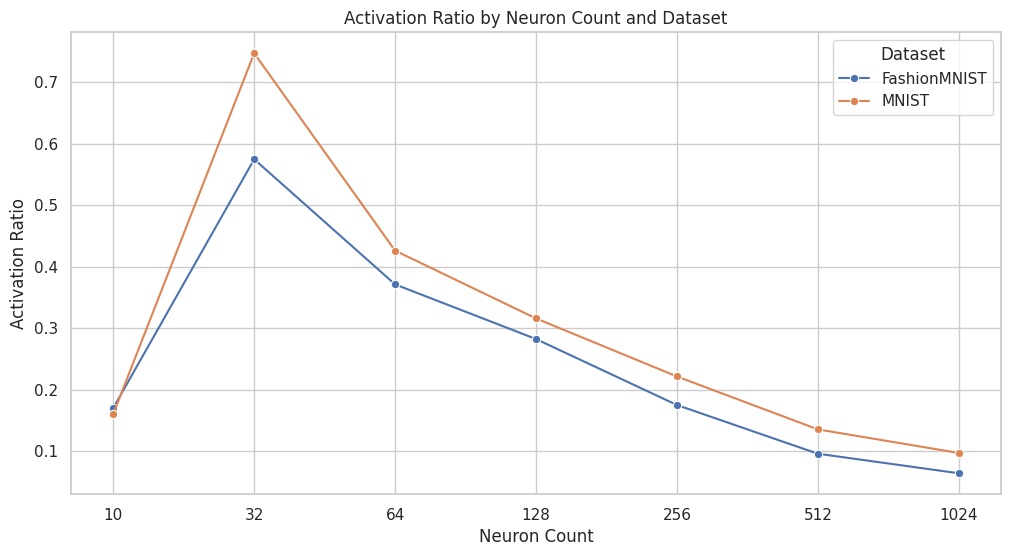
Let's explore the activation ratios of a simple feedforward network with various layer sizes and dimensions for the MNIST handwritten digit recognition and FashionMNIST datasets.

The network architectures tested were as follows, with each layer being a linear layer (without bias) and ReLU as the activation function: 784 => 512 => 256 => 128 => 64 => 10; 784 => 256 => 128 => 64 => 10; 784 => 128 => 64 => 10; 784 => 512 => 128 => 10; 784 => 1024 => 256 => 64 => 10; 784 => 64 => 32 => 10

Source code at github (Open in Colab)
Activation ratio data: mnist.csv, gpt.csv

When analyzing the relationship between activation ratios and layer size, we see a significant decrease in activation ratio as layers get bigger. The final layer, with 10 neurons, is an exception since this network is trained as a classifier, meaning only one neuron should be activated, resulting in an expected activation ratio of around 10%. While different datasets cause slight variations in activation ratios, the overall trend remains consistent across both datasets.

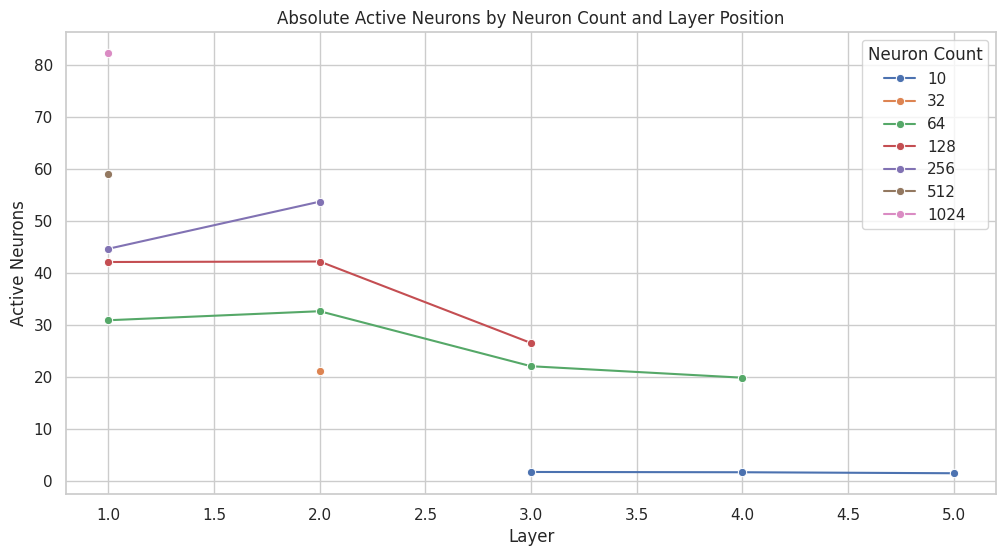
When considering the absolute count of active neurons relative to layer size, doubling the dimension results in only a slight increase in the absolute activation count.

Neuron Count	Absolute	Predicted	Activation Ratio (%)
10	2	10	17.2%
32	17	18	54.6%
64	25	26	38.4%
128	35	36	27.3%
256	47	51	18.2%
512	50	72	9.7%
1024	64	102	6.3%

By fitting this data to a curve, we can estimate the number of active neurons using the formula:

$A = F \times \sqrt{N}$

where:
$A$ is the estimated number of activated neurons,
$N$ is the neuron count of the layer,
$F$ is the fit factor (approximately 3.6 for MNIST, 3.2 for FashionMNIST).

This diminishing number of activated neurons might suggest that the neural network is running out of meaningful features it can learn. While validation accuracy generally improves with larger layers, it tends to plateau after a certain point, so that could be one of the reasons why the activation ratio only slightly increases when using bigger layers.

When investigating how a layer's position affects its activation ratio, the limited data suggests that the number of active neurons decreases a bit as a layer with the same dimension is placed deeper within the neural network.

Transformers

Given the significance of the largest models available today, I'm also interested in the activation ratio in the MLP layers of a transformer. Here, we focus on the activation layers of the feedforward neural network after it projects into the higher-dimensional space. Although we use the GELU function as the activation, we'll assume a neuron is activated if it outputs a value greater than zero, like we did with ReLU activations.
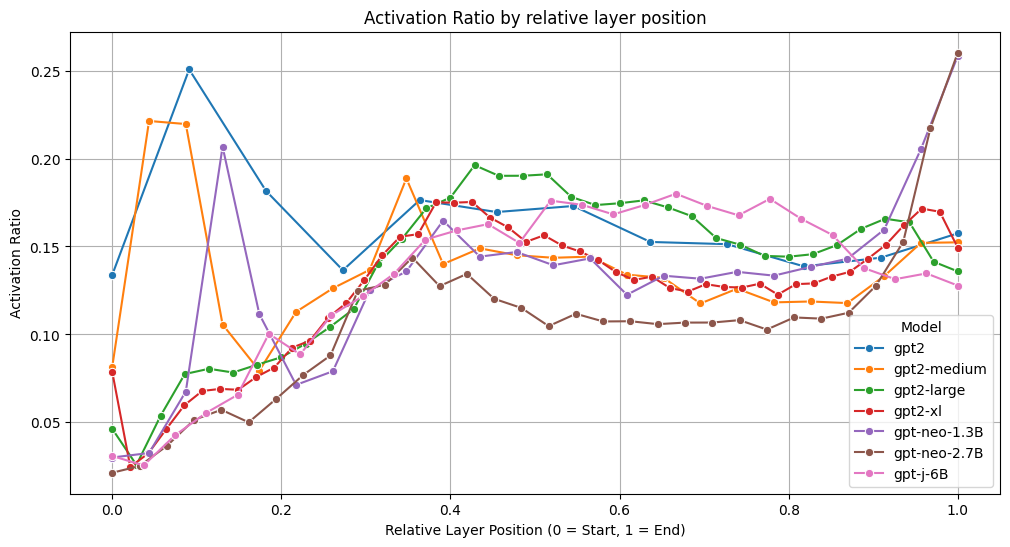
The activation ratio is averaged over 4 prompts.

We observe that the activation ratio begins at around 4% in most models and rises over the first 1/3 of the layers to about 14%, where it remains for the final 2/3 of the layers. While there are some variations among the models, they tend to follow this trend.

Conclusion

• In classification models, only a small fraction of neurons in a layer are activated. Increasing the layer's dimension only slightly increases the number of activated neurons.
• In Transformers, the activation ratio remains fairly constant around 14% (ranging from 11% to 18%) for the last 2/3 of the layers, while it linearly increases from 4% to 14% (in most tested models) for the first 1/3 of the layers.

A massive amount of compute is wasted in large layers.

There may be considerable performance gains waiting to be exploited.
I'm actively working on this, with more updates to come in the next blog post.

Future work I don't have time for:

• How does a wider variety of model architectures perform (e.g., Llama 3.1)?
• How does the activation ratio change over training (initially starts at 50%)?
• What is the impact of the GELU activation in transformers?
• Is the decreasing activation ratio in larger layers due to running out of features to learn?
• Does the estimation formula work for all classification tasks?

You can comment on this blog post here.